Density-based novelty detection
General ·Novelty Detection이란?
Novelty detection은 일반적인 데이터의 경향과는 다른 특이한 혹은 이상한 데이터(novel data, outliers)를 찾아내는 기술입니다. 예를 들어 갑자기 어떤 신용카드가 여태까지 쓰이지 않던 장소에서 쓰이지 않던 방식으로 쓰였다면 이것은 ‘이상한 데이터’라고 할 수 있습니다. Novelty detection은 이런 식의 이상성을 발견하고자 하는 알고리즘입니다.
“Observations that deviate so much from other observations as to arouse suspicions that they were generated by a different mechanism (Hawkins, 1980)” “Instances that their true probability density is very low (Harmelinget al., 2006)”
위에서 정의된 것처럼 novel data(outliers)는 일반적인 데이터와 차이가 많이 나는 관측 데이터라고 볼 수 있습니다. 여기서 재밌는 점은 novel data는 noise data와 다르다 는 점입니다. Noise는 데이터 전처리 과정에서 제거해줘야 할 데이터이기 때문에 novelty detection 이전에 제거하게 됩니다. 하지만 novel data는 일반적인 데이터를 만들어낸 메커니즘을 위반하는 특이한 케이스의 관측치들이기 때문에 novelty detection에서 찾아내고자 하는 관측치입니다.
Novel data의 종류
Novel data에는 크게 세 종류가 있습니다.
- Global Outlier
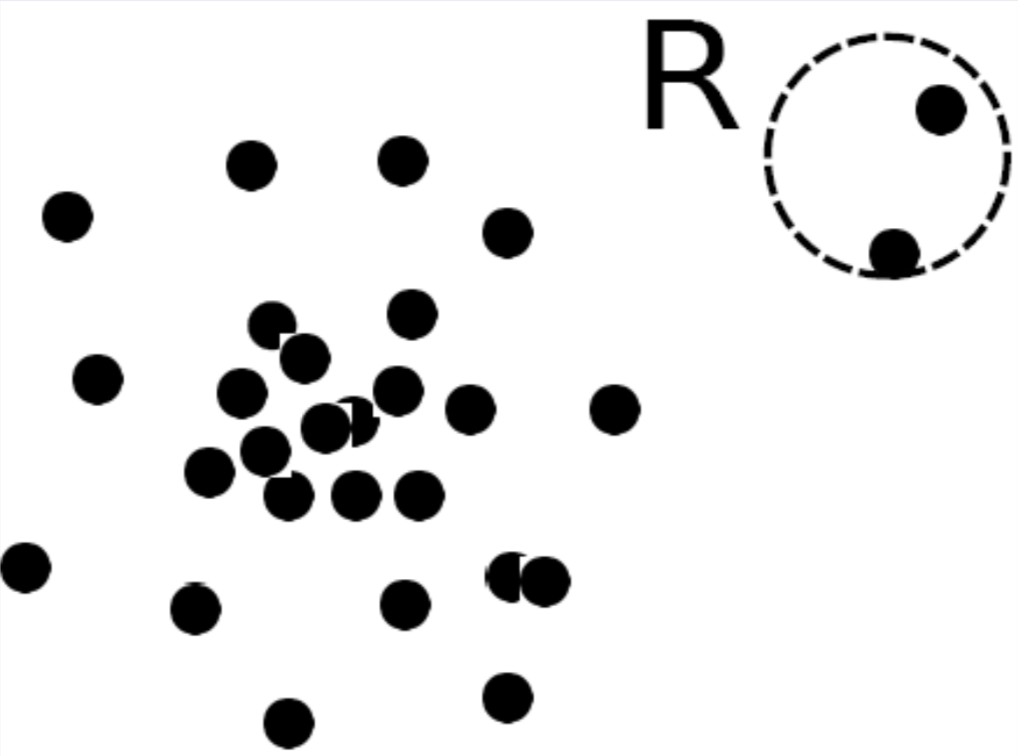
우리가 보는 일반적인 “outlier”라고 할 수 있습니다. 단순히 일반적인 관측치와 동떨어진 관측치들입니다.
- Contextual outlier(local outlier)
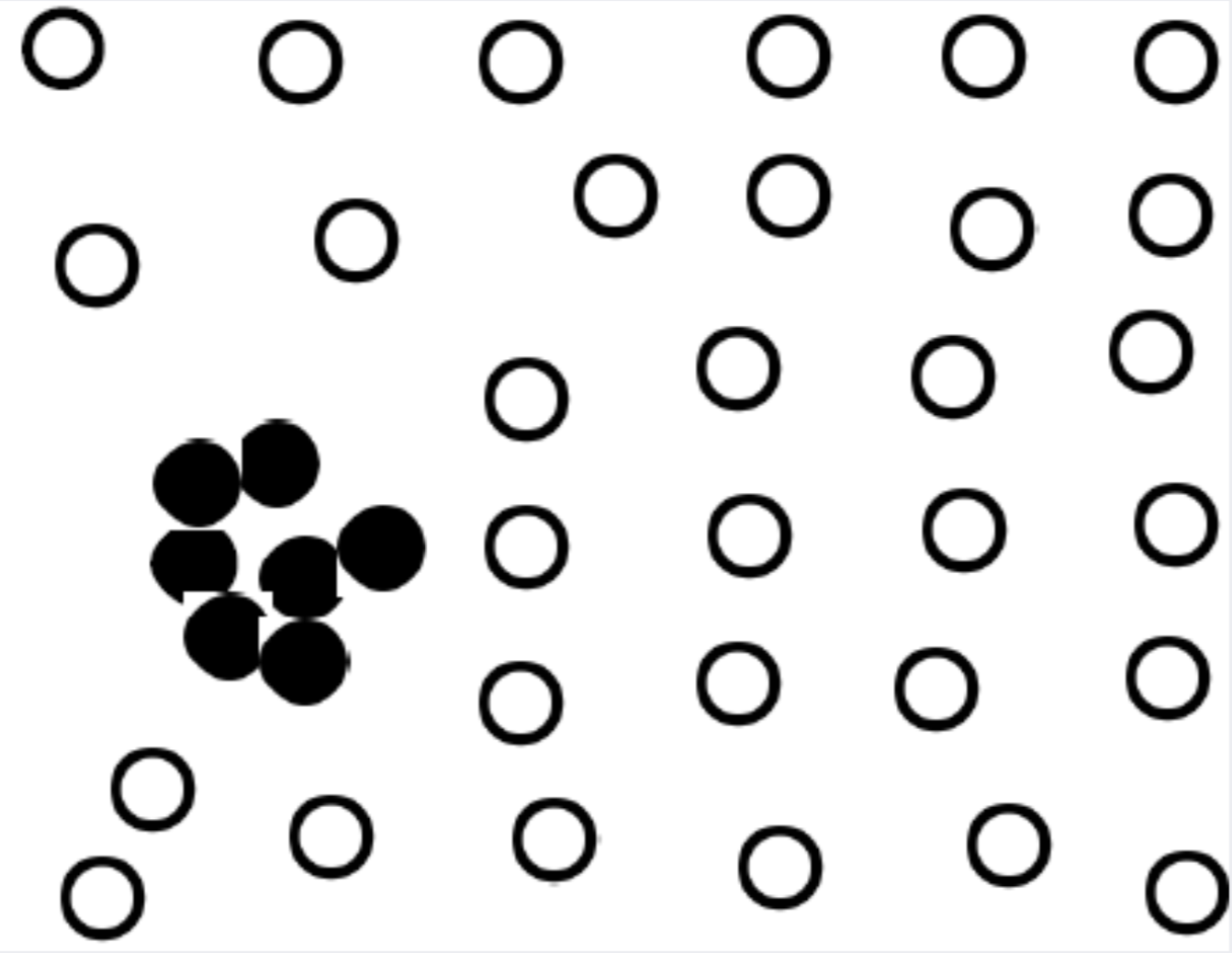
특정 상황 혹은 맥락 정보를 고려해 “outlier”가 되는 경우입니다. 예를 들면, 알래스카의 영상 30도는 outlier라고 볼 수 있지만, 사하라 사막의 영상 30도는 outlier가 아닐 수 있습니다.
- Collective outlier
개별적인 관측치들이 outlier가 아니더라도, 데이터의 부분집합이 집단적으로 전체 데이터로부터 동떨어진 움직임이 있다면 이것을 collective outlier라고 합니다. 대표적으로 Dos attack이 있습니다.
Classification과의 차이
Novelty Detection은 Classification과 차이가 있습니다.
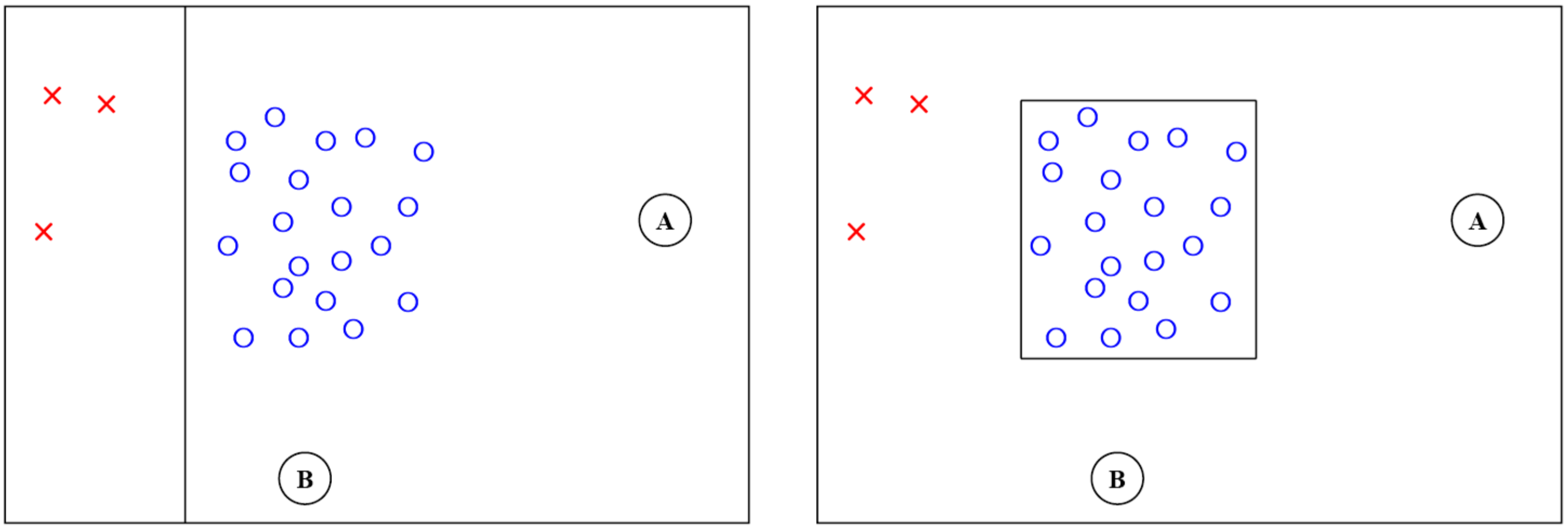
왼쪽의 그림에서처럼 Classification은 X와 O를 각각 X의 경우에는 “빨간색”의 범주로, O의 경우에는 “파란색”의 범주로 학습시킵니다. 즉, 각각의 범주를 학습시킵니다. 반면 오른쪽의 그림에서처럼 Novelty detection은 파란색만 데이터로 활용해 훈련해서, 결과적으로 파란색(정상) 범주에 포함되는지 포함되지 않는지만을 알아내는 것이 목적입니다.
Class Imbalance가 크고, minority class example의 개수가 충분하지 않을 때 우리는 novelty detection 알고리즘을 사용하고, 만약 class간의 imbalance가 크더라도 minority class example 데이터의 절대량이 크다면 비율을 맞춰서 classification 방식으로 훈련하는 것이 적합합니다. 즉, novelty detection은 classification 방식이 불가능할 때 대안 방법으로 사용할 수 있습니다.
Performance measure
Novelty detection 알고리즘의 평가는 다음과 같이 합니다.
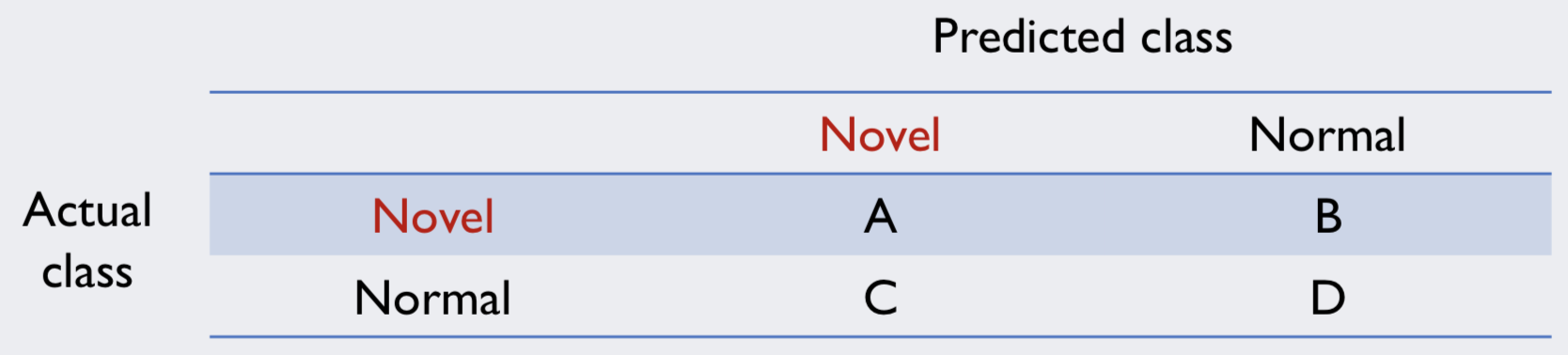
우선 normal data를 novel data로 분류한 경우와, novel data를 normal data로 분류한 경우가 적을 수록 이상한 데이터를 잘 가려내었다고 판단할 수 있습니다.

normal data를 novel data로 분류한 경우의 에러는 False Rejection Rate(FRR)로 표현할 수 있고, novel data를 normal data로 분류한 경우의 에러는 False Acceptance Rate (FAR)로 표현할 수 있습니다.
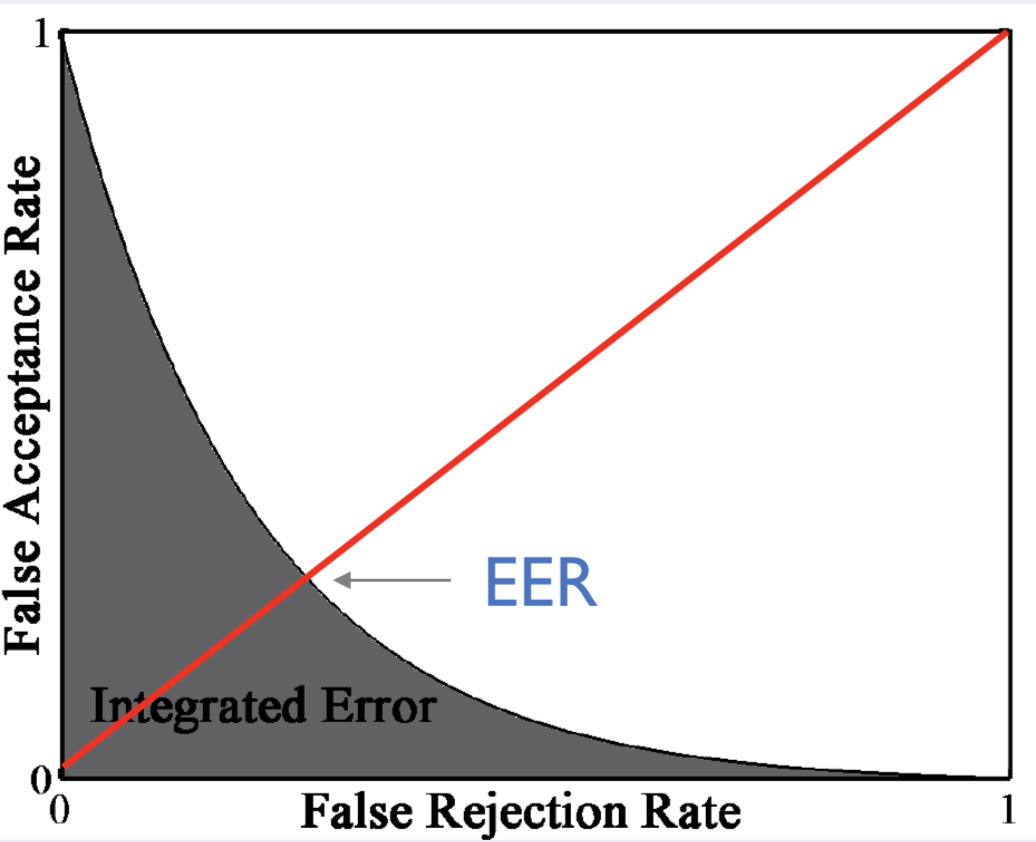
FRR과 FAR을 두 축으로 해서 FRR이 FAR과 같아질 때를 Equal error rate(EER)이라고 하고, FRR-FAR curve의 밑부분의 면적을 Integrated Error(IE)라고 합니다. Novelty detection 알고리즘은 EER과 IE가 낮을수록 좋다고 평가할 수 있습니다.
Density-based Novelty Detection
Density-based 방식은 기존에 가지고 있는 정상 데이터의 분포를 사용하여 outlier를 찾아내는 방식입니다. 기존에 있는 데이터를 사용하여 알고리즘을 학습하기 때문에 supervised learning이라고 할 수 있습니다.
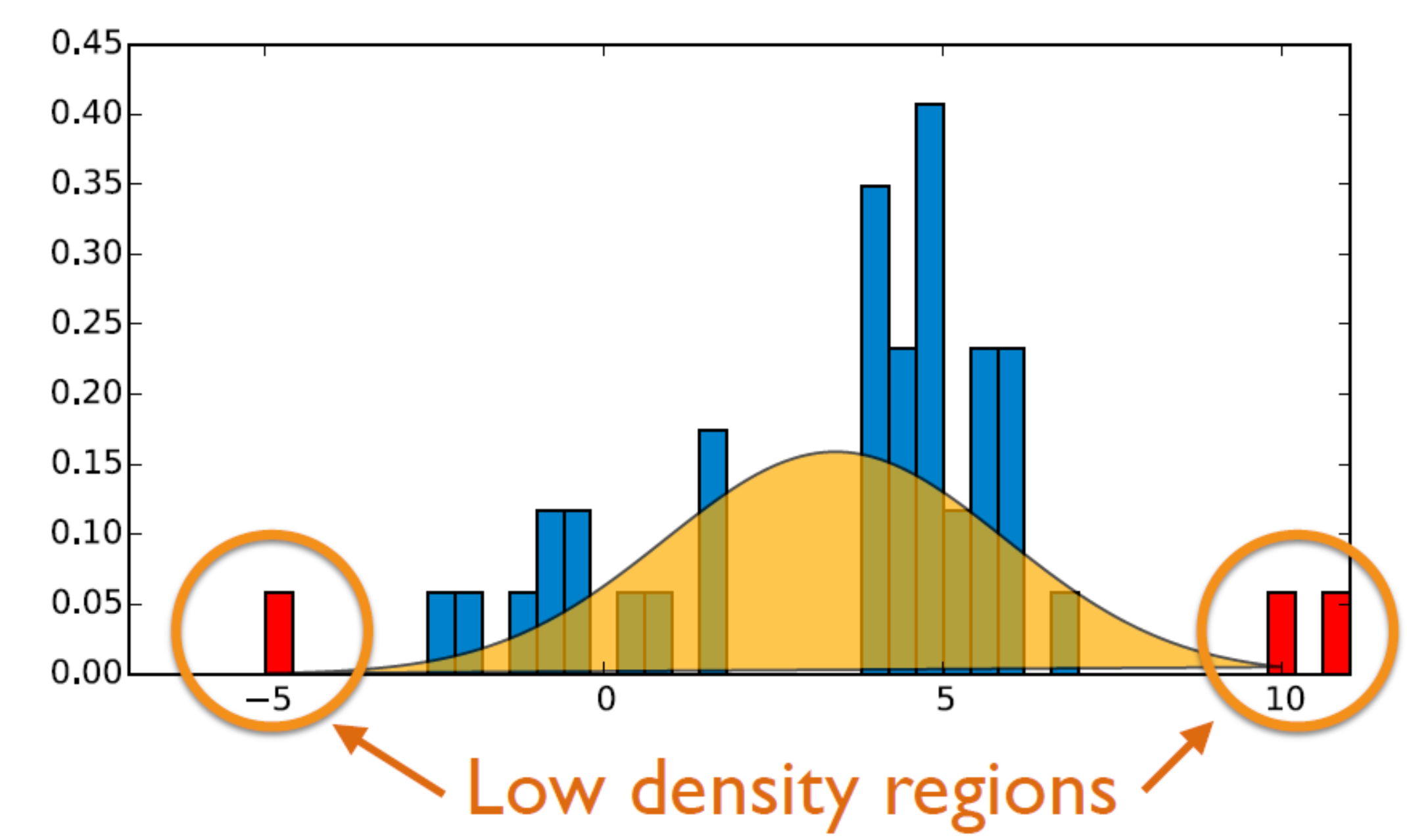
위 그림에서 보시다시피, 우리가 갖고 있는 정상 데이터 분포가 있을 경우에 빨간색 데이터가 들어온다면 이는 outlier라고 할 수 있습니다. 이렇듯 정상 데이터만을 사용하여 추정한 분포를 가지고 이상치를 탐지할 수 있습니다.
앞으로 설명할 밀도 기반 이상치 탐지 기법은 총 4개입니다.
- Gaussian Density Estiation
- Mixture of Gaussian Density Estimation
- Kernel-density Estimation
- Local Outlier Factors (LOF)
Gaussian Density Estimation
가우시안 밀도 추정 방법은 우리가 가진 정상 데이터의 분포가 기본적으로 가우시안 분포(정규 분포)를 따른다고 가정하는 방법입니다.
이 식은 우리가 익히 보아온 가우시안 분포를 표현한 식입니다. 여기서 각각 mu와 sigma는 아래의 식과 같습니다.
여기서 X+는 정상 데이터를 의미합니다.
Maximum likelihood estimation
데이터의 각 값들이 나올 확률을 가장 잘 설명하는 분포가 그 데이터의 가우시안 분포라고 할 수 있습니다. 왜냐하면 실제 관측값이 측정될 각각의 확률들을 곱했을 때 최대가 되게끔 하는 분포가 그 데이터의 가우시안 분포이기 때문입니다. 이를 밑의 식으로 표현할 수 있습니다.
여기에 로그를 씌우면 밑의 식과 같이 됩니다.
식을 더 쉽게 표현하기 위해 $\gamma =\frac { 1 }{ { \sigma }^{ 2 } }$로 바꿔서 표현하면 다음과 같습니다.
Log-likelyhood는 아시다시피 위로 볼록한 함수입니다. 이러한 이유 때문에 미지수인 $\mu $와 $\gamma $에 대해 일차 미분을 해서 최적값을 구할 수 있습니다.
위의 식을 통해서 우리가 가진 데이터의 평균과 분산이 정규분포의 평균과 분산과 같아지는 것을 확인할 수 있었습니다.
가우시안 분포는 Covariance matrix type에 따라 모양이 변합니다.
- Spherical type
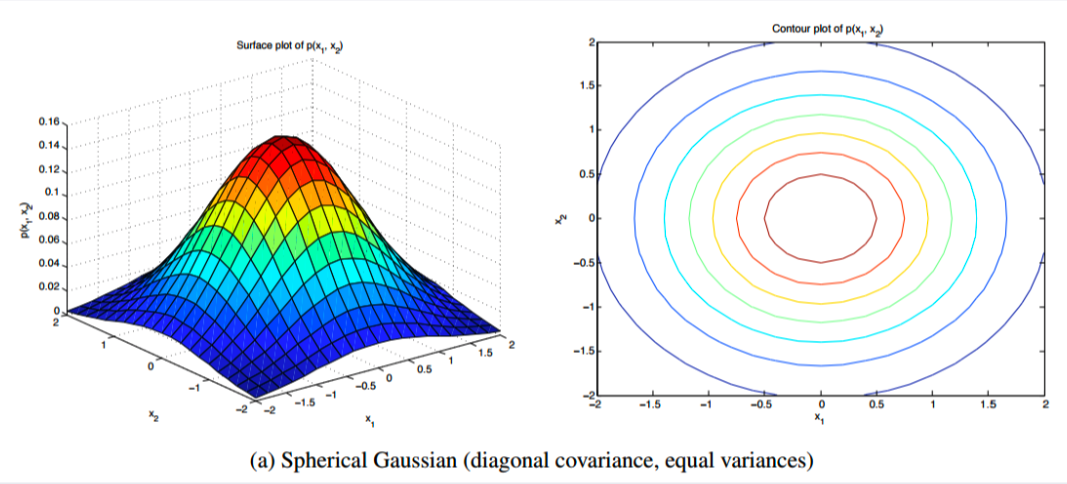
covariance matrix가 diagonal이고 동시에 x1과 x2의 각 축에서 분산이 같다고 단순하게 가정했을 때의 가우시안 분포는 위에서 봤을 때 원모양의 등고선을 보여줍니다.
- Diagonal type
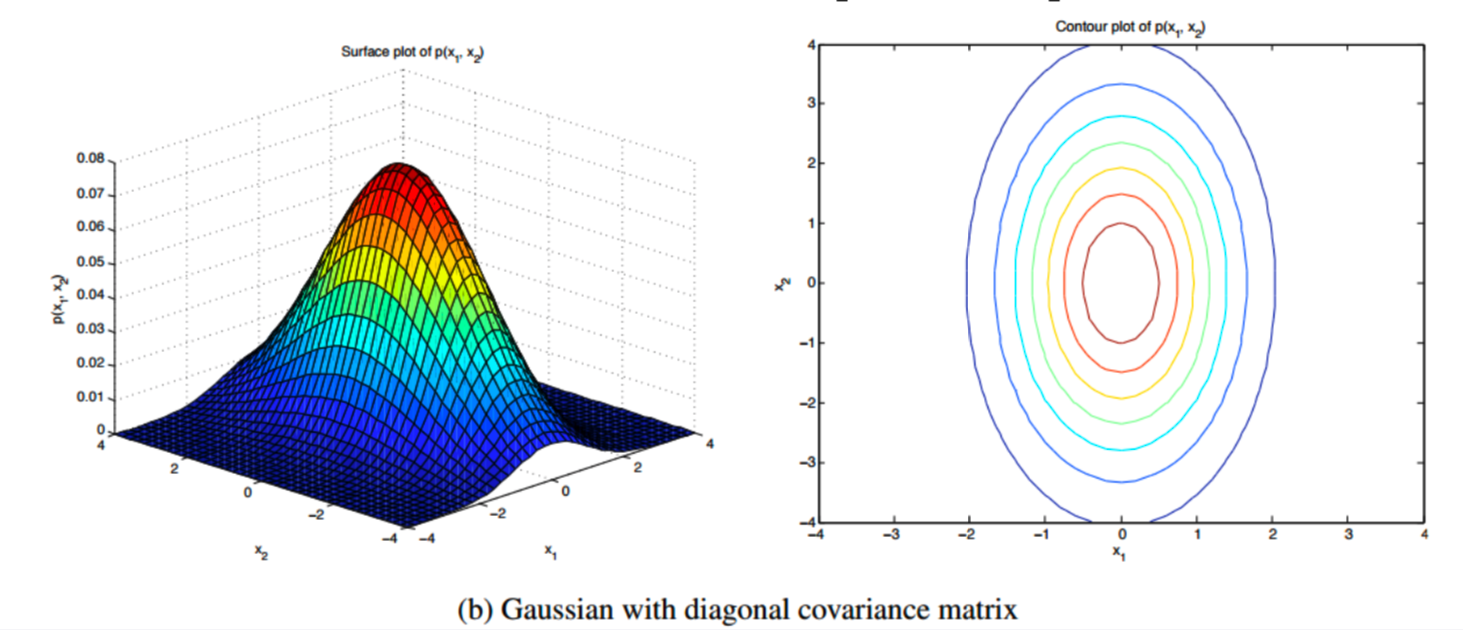
covariance matrix가 diagonal이긴 하지만 축마다 분산이 다르다고 가정한 경우의 가우시안 분포는 위에서 봤을 때 축이 어그러지지 않은 타원형의 등고선을 보여줍니다.
- Full type
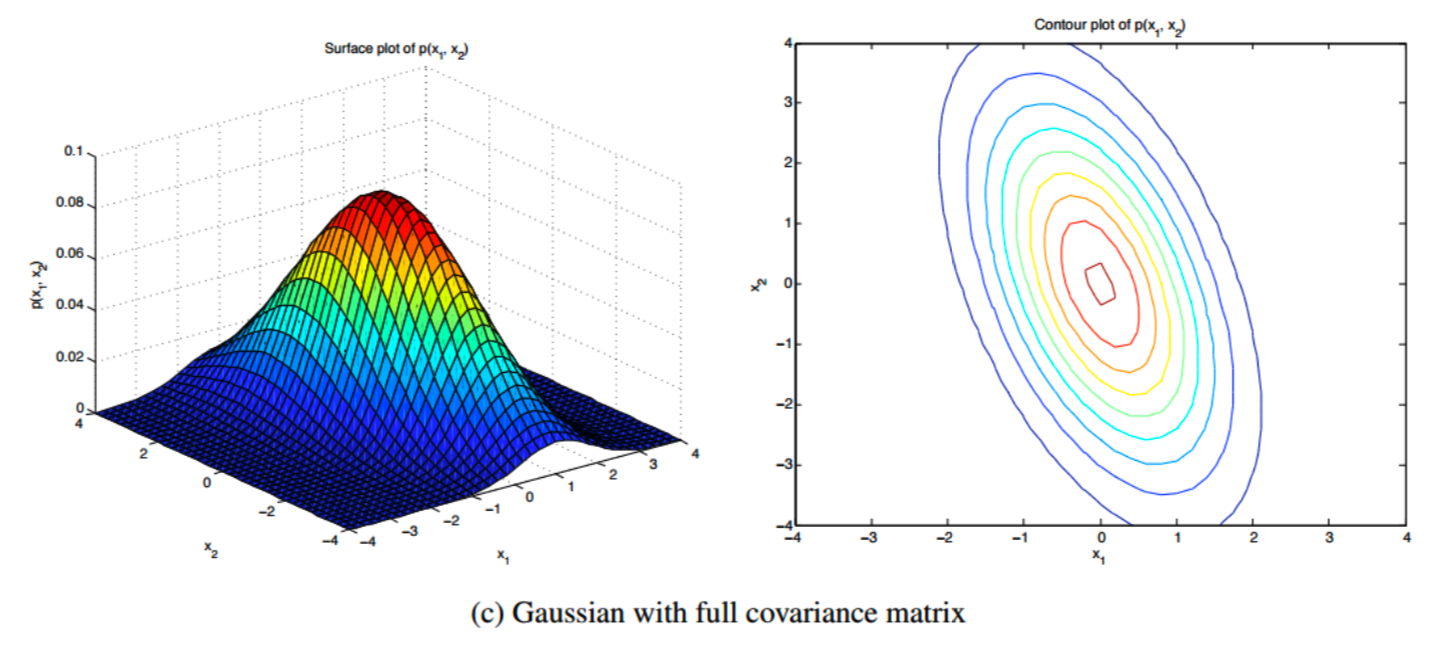
full covariance matrix를 가질 때를 가정하면 가우시안 분포가 축도 어그러진 타원형의 등고선을 보이고 있습니다.
아래는 가우시안 밀도 추정을 코드로 구현한 예시입니다.
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import math
#### generate some arbitrary data
mu, sigma = 3, 2
data = np.random.normal(mu, sigma, 100)
##### plot data
plt.plot(data, np.zeros_like(data), 'x')
# data driven mu and sigma
print("Data driven mu=" , np.mean(data))
print("Data driven sigma=", np.std(data))
### x축
x = np.linspace(start=-5, stop=8, num=1000)
### uni-gaussian pdf 의 y 좌표
uni_g = stats.norm(np.mean(data), np.std(data)).pdf(x)
plt.plot(x,uni_g)
plt.show()
### 정상 데이터 개수
n=0
### 비정상 데이터 개수
m=0
for i in range(len(data)):
if (stats.norm(np.mean(data), np.std(data)).pdf(data[i])) > 0.05 and \
(stats.norm(np.mean(data), np.std(data)).pdf(data[i])) < 0.995:
n=n+1
else:
print(data[i],"= outlier")
m=m+1
print("정상 데이터 개수:",n)
print("비정상 데이터 개수:",m)
Mixture of Gaussian
위에서 본 Gaussian Density Estimation은 데이터의 분포가 가우시안 분포를 따른다는 강한 가정을 하고 있기 때문에, 복잡한 데이터의 분포의 경우는 잘 표현하지 못할 수 있습니다. 이런 이유 때문에 여러개의 가우시안 분포의 결합으로 데이터 분포를 나타내고자 하는 알고리즘이 바로 Mixture of Gaussian(혼합 가우시안) 알고리즘이라고 할 수 있습니다.
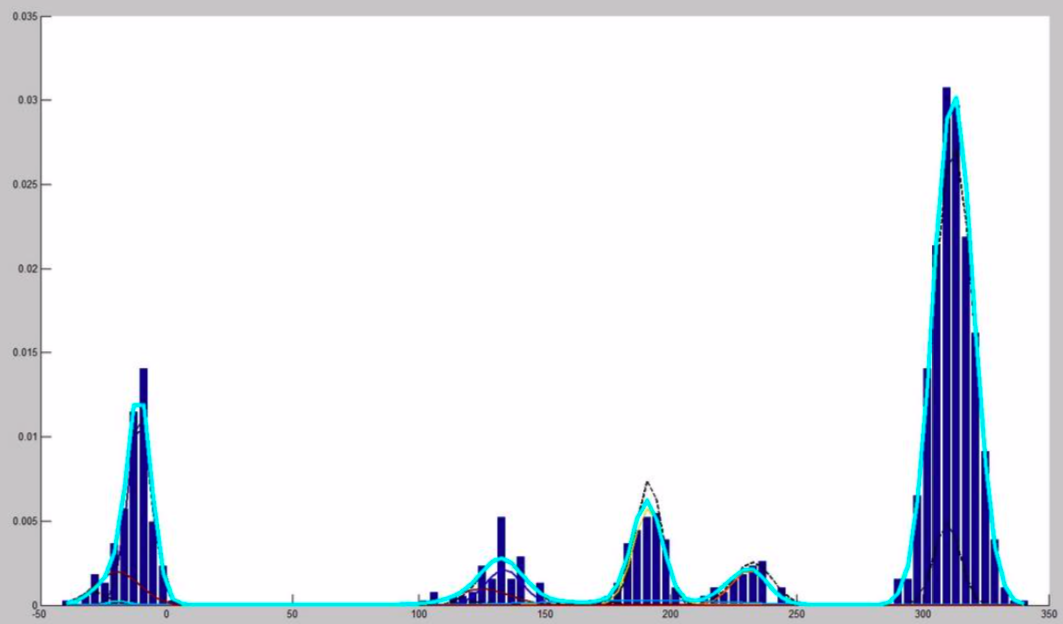
혼합 가우시안 분포에서 데이터가 normal일 확률은 다음과 같습니다.
이 때 g와 lamda는 다음과 같습니다.
즉 M개의 가우시안 분포를 가정하고 있고, 각각의 가우시안 분포에 가중치를 주어서 전체 분포를 추정하고 있습니다.
Expectation-Maximization Algorithm
혼합 가우시안 모델을 쓰기 위해서는 Expectation-Maximization Algorithm을 사용해야 합니다. 이 때, Expectation은
를 고정시킨 상태에서 m을 찾는 과정입니다. 이 때, m은 개별 개체가 몇 번 분포에 얼마만큼 들어갈 확률인지를 말합니다.
Maximization은 m을 고정한 상황에서
를 최적화하는 과정입니다.
EM 알고리즘은 이 두 과정을 계속적으로 반복해 나가면서 데이터의 분포를 추정하고자 합니다.
혼합 가우시안 분포도 역시 어떻게 Covariance matrix type을 가정하느냐에 따라 모양이 변합니다.
아래는 혼합 가우시안 분포를 통해 novelty detection을 하는 코드의 예제입니다.
import numpy as np
import pandas as pd
import random as rand
import matplotlib.pyplot as plt
import scipy as sc
from scipy.stats import norm
from sys import maxsize
class GMM:
def __init__(self, dataframe, parameters):
self.dataframe = dataframe.copy()
self.new_dataframe = dataframe.copy()
self.parameters = parameters.copy()
self.new_params = parameters.copy()
def p(self, val, mu, sig, lam):
p = lam
for i in range(len(val)):
p *= norm.pdf(val[i], mu[i], sig[i][i])
return p
def expectation(self):
for i in range(self.dataframe.shape[0]):
x = self.dataframe['x'][i]
y = self.dataframe['y'][i]
cluster1 = self.p([x, y], list(self.parameters['mu1']), list(self.parameters['cov1']), self.parameters['lambda'][0])
cluster2 = self.p([x, y], list(self.parameters['mu2']), list(self.parameters['cov2']), self.parameters['lambda'][1])
if cluster1 > cluster2:
self.new_dataframe['label'][i] = 1
else:
self.new_dataframe['label'][i] = 2
# update estimates of lambda, mu and sigma
def maximization(self):
cluster1_points = self.new_dataframe[self.new_dataframe['label'] == 1]
cluster2_points = self.new_dataframe[self.new_dataframe['label'] == 2]
percent_assigned_to_cluster1 = len(cluster1_points) / float(len(self.new_dataframe))
percent_assigned_to_cluster2 = 1 - percent_assigned_to_cluster1
self.new_params['lambda'] = [percent_assigned_to_cluster1, percent_assigned_to_cluster2]
self.new_params['mu1'] = [cluster1_points['x'].mean(), cluster1_points['y'].mean()]
self.new_params['mu2'] = [cluster2_points['x'].mean(), cluster2_points['y'].mean()]
self.new_params['cov1'] = [[cluster1_points['x'].std(), 0], [0, cluster1_points['y'].std()]]
self.new_params['cov2'] = [[cluster2_points['x'].std(), 0], [0, cluster2_points['y'].std()]]
def distance(self):
difference = 0
for param in ['mu1', 'mu2']:
for i in range(len(self.parameters)):
difference += (self.parameters[param][i] - self.new_params[param][i]) ** 2
return difference ** 0.5
def update(self):
self.dataframe = self.new_dataframe.copy()
self.parameters = self.new_params.copy()
def check_novelty(self):
for i in range(self.dataframe.shape[0]):
x = self.dataframe['x'][i]
y = self.dataframe['y'][i]
cluster1 = self.p([x, y], list(self.parameters['mu1']), list(self.parameters['cov1']), self.parameters['lambda'][0])
cluster2 = self.p([x, y], list(self.parameters['mu2']), list(self.parameters['cov2']), self.parameters['lambda'][1])
if (cluster1 + cluster2) < 0.001:
print(i ,'번째 샘플 :', [x, y] , 'prob :', cluster1+cluster2)
#### generate 2 clusters
### cluster 1
mu1 = [0, 5]
cov1 = [ [2, 0], [0, 3] ]
num1 = 100
### cluster2
mu2 = [5, 0]
cov2 = [ [4, 0], [0, 1] ]
num2 = 100
data1 = np.random.multivariate_normal(mu1, cov1, num1)
x1, y1 = data1.T
data2 = np.random.multivariate_normal(mu2, cov2, num2)
x2, y2 = data2.T
### concatenate all samples
xs = np.concatenate((x1, x2))
ys = np.concatenate((y1, y2))
labels = ([1] * num1 + [2] * num2)
data = {'x': xs, 'y': ys, 'label': labels}
df = pd.DataFrame(data)
# initial guesses
guess = { 'mu1': [1,1],
'cov1': [ [1, 0], [0, 1] ],
'mu2': [4,4],
'cov2': [ [1, 0], [0, 1] ],
'lambda': [0.5, 0.5]
}
params = pd.DataFrame(guess)
# loop until parameters converge
#### setup before iteration
shift = maxsize
epsilon = 0.01
iternum = 0
# randomly assign points
df_copy = df.copy()
df_copy['label'] = map(lambda x: x+1, np.random.choice(2, len(df)))
gmm = GMM(df_copy.copy(), params)
while shift > epsilon:
iternum += 1
# E-step
gmm.expectation()
# M-step
gmm.maximization()
# how much change
shift = gmm.distance()
print("iteration {}, shift {}".format(iternum, shift))
gmm.update()
fig = plt.figure()
plt.scatter(gmm.dataframe['x'], gmm.dataframe['y'], c=gmm.dataframe['label'])
fig.savefig("iteration{}.png".format(iternum))
gmm.check_novelty()
Kernel Density Estimation
커널 밀도 추정은 데이터가 가우시안 분포와 같은 특정 분포를 따르지 않는다고 가정합니다. 즉, 데이터 자체에서 바로 밀도 추정을 하고자 시도하는 방법입니다.
p(x)(임의의 확률 밀도 함수)의 분포에서 벡터 x가 표본 공간에 주어진 R 범위에 있을 확률은 밑 식처럼 나타낼 수 있습니다.
N 개의 벡터 ${ { x }^{ 1 },{ x }^{ 2 },… ,{ x }^{ n }}$ 가 p(x)의 분포에서 추출된 벡터들이라고 생각해봅시다. 이 N개의 벡터들 중 k개의 벡터가 R에 들어갈 확률은 다음과 같습니다.
이는 이항분포이므로, k/N의 평균과 분산 값을 다음과 같이 찾을 수 있습니다.
이 식에서 N이 무한대로 가면, 분산은 0에 가까워지게 되고 결국 $P\cong \frac { k }{ N }$ 식이 성립될 것입니다.
R이 만약 엄청 작아지게 된다면 $P=\int _{ R }^{ }{ P({ x }^{ \prime })d{ x }^{ \prime } } \cong p(x)V=\frac { k }{ N } ,\quad p(x)=\frac { k }{ NV }$ 의 식이 성립하게 됩니다.
이 식에서 우리가 가져야 하는 조건은 첫번째로, R이 충분히 작아야 한다는 것과, 두번째로, 그럼에도 불구하고 N개 벡터 중 K개가 R에 들어갈 정도로는 커야한다는 것입니다. 이를 V를 고정시키고 k를 결정하는 문제로 본 것이 Kernel-density Estimation입니다.
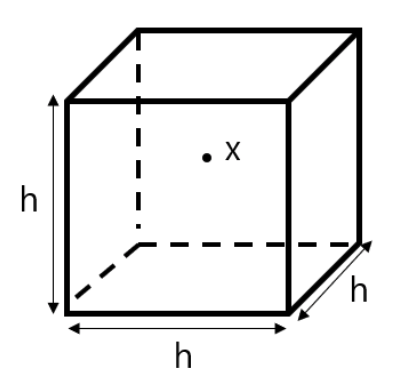
k개의 샘플을 갖고 있는 hypercube의 영역 R이 있다고 가정해봅시다. 이 hypercube 의 한 변의 길이를 h라고 하고, 이 hypercube의 정 중앙을 x라고 합시다. 이 때, 차원이 d라면 이 영역의 부피는 ${ h }_{ n }^{ d }$ 입니다.
만약 이 큐브 안에 샘플 개수를 세는 식을 만든다면, 밑 식과 같습니다.
이 식은 결국 x를 기준으로 각 차원에서 h/2 거리 안에 있는 모든 샘플의 개수를 세고 있는 식입니다. 위와 같은 함수를 Kernel Function(커널 함수)라고 합니다. (이 경우엔 Parzen window(파젠 윈도우)를 예시로 한 것입니다.)
Parzen 윈도우를 통해 데이터의 밀도를 추정한 함수는 다음과 같습니다.
지금 이 경우는 파젠 윈도우를 사용한 것이지만, 파젠 윈도우는 영역 안은 무조건 1 값을, 영역 밖이면 무조건 0 값을 주고 있기 때문에 밀도 표현이 불연속적이게 됩니다. 이러한 이유 때문에 다양한 방식의 다른 커널을 사용하기 합니다.
대표적으로 가우시안 커널을 사용하는 경우에는 밑의 식처럼 표현할 수 있습니다.
또한 h값에 따라 추정하느 분포의 모양이 달라지는데요, h가 큰 값일 경우 완만한 분포가 추정되고, h가 작은 값일 경우에는 뾰족뾰족한 분포가 됩니다.
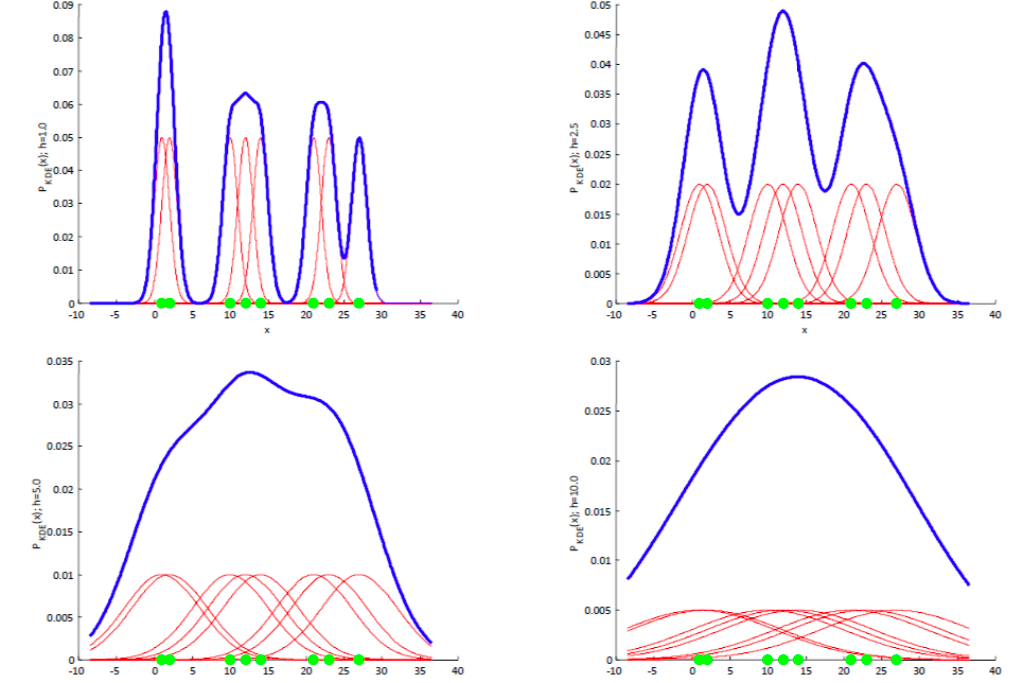
Local Oultlier Factors
Local Outlier Factors(LOF)는 데이터가 가지는 상대적인 밀도까지 고려한 이상치 탐지 방법입니다.
LOF에서는 k-distance라는 개념을 사용합니다. k-distance(p)란 A 데이터로부터 k번째로 가장 가까운 데이터까지의 거리를 뜻합니다. 그리고 그 때 k-distance 범위 내에 들어오는 데이터의 집합을 ${N}_{k}(p)$ 라고 합니다.
LOF에서는 reachability distance라는 것도 정의해야 합니다.
reachability distance는 단순하게 말하자면, k-distance 범위 안에 있는 데이터까지의 거리는 p와 o 사이의 거리와 k-distance 중 큰 값을 사용하자는 것입니다.
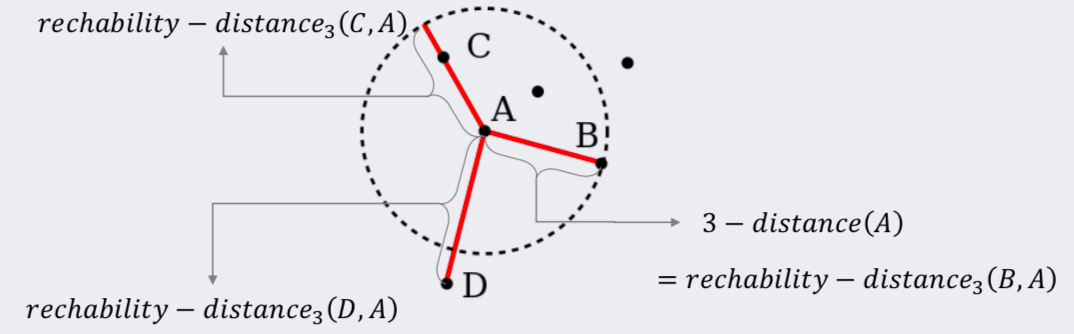
위에서 보면 A에서 C까지의 거리를 rechability distance로 바꾸어서 거리를 계산하게 되면 3-distance(A)와 같아집니다. D의 경우는 rechability distance보다 멀리 있기 때문에 그대로 거리값을 사용하게 됩니다.
Local reachability distance는 다음과 같이 정의합니다.
분자는 k-distance 안의 개체 수이고, 분모는 p에서 다른 오브젝트까지의 reachability distance입니다.
p가 밀도가 높은 부분에 위치한다면 분모는 작아지게 되고, 그러면 ${lrd}_{k}(p)$ 값은 커집니다.
반대로 p가 밀도가 낮은 부분에 위치한다면 분모는 커지고, 그러면 ${lrd}_{k}(p)$ 값은 작아집니다.
Local outlier factor
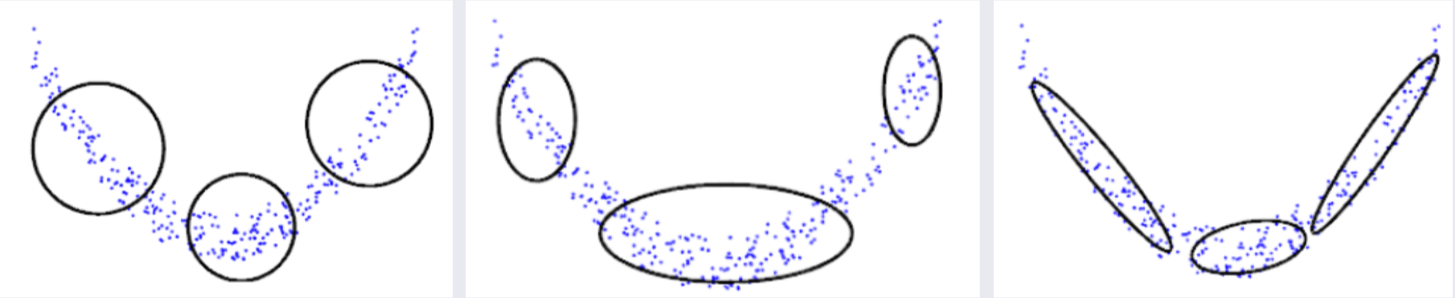
LOF 점수는 위의 식처럼 구할 수 있습니다. 여기서 LOF의 점수는 p가 얼마나 이상치인지를 나타내주는 점수라고 할 수 있습니다.
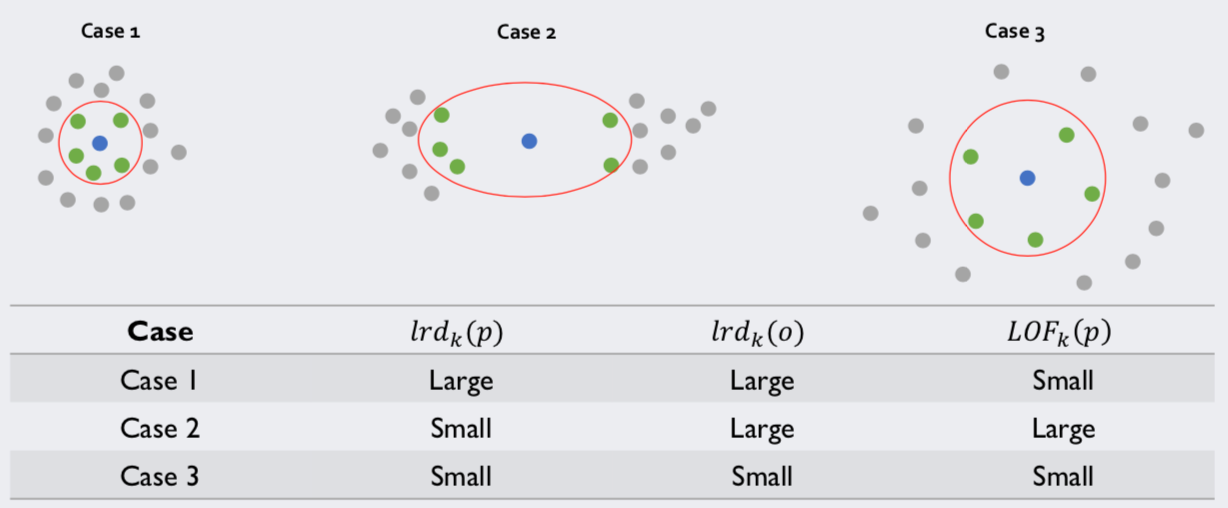
위 그림에서 파란색 점이 p이고 초록색 점이 q라고 합시다. LOF(p) 값이 크려면 ‘초록색 점들이 밀도가 높은 와중에 파란색 점은 밀도가 낮아야’ 합니다. 지금 Case 2번의 경우만 이런 조건을 만족시키기 때문에 LOF(p)가 높고, 나머지 케이스들은 LOF(p)가 낮습니다.
즉, 단순히 파란색 점 주변의 상대적 밀도뿐만 아니라 초록색 점 주변의 상대적 밀도들도 같이 고려해주는 알고리즘입니다.
아래는 novelty detection을 하기 위해 LOF 점수를 계산하는 코드의 예제입니다.
import numpy as np
import scipy.spatial as sc
import pandas as pd
import random
class LOF:
def __init__(self, data, nkp):
self.nkp = nkp
self.data = data
self.index = len(data)
self.dist_list = []
self.k_dist_list = []
self.points_in_circle_list = []
self.lrd_list = []
def k_dist(self):
df = pd.DataFrame(self.data, columns=['X', 'Y'], index=range(self.index))
distance = pd.DataFrame(sc.distance_matrix(df.values, df.values),
index=df.index, columns=df.index)
dist_list = []
k_dist_list = []
for i in range(0, self.index):
dist = np.array(distance[i])
dist = np.delete(dist, [i])
self.dist_list.append(dist)
sorted_dist = np.array(distance[i])
sorted_dist = np.delete(sorted_dist, [i])
sorted_dist.sort()
k_distance = sorted_dist[self.nkp - 1]
self.k_dist_list.append(k_distance)
return
def reachability_dist(self):
points_in_circle_list = []
for i in range(0, self.index):
points_in_circle = np.where(self.dist_list[i] <= self.k_dist_list[i])
self.points_in_circle_list.append(points_in_circle)
points_in_circle_ints = points_in_circle[0]
for j in points_in_circle_ints:
self.dist_list[i][j] = self.k_dist_list[i]
return
def lrd(self):
for i in range(0, self.index):
lrd_p = (self.nkp) / sum(self.dist_list[i][self.points_in_circle_list[i][0]])
self.lrd_list.append(lrd_p)
return
def LOF_score(self):
a = 0
lrd_neighbors=[]
LOFscore = []
for i in range(self.index):
points_in_circle = self.points_in_circle_list[i]
for j in range(len(points_in_circle[0])):
points_in_circle_ints = points_in_circle[0]
a = a + self.lrd_list[points_in_circle_ints[j]]
lrd_neighbors.append(a)
a = 0
for i in range(0, self.index):
lof = (lrd_neighbors[i] / self.lrd_list[i]) / self.nkp
LOFscore.append(lof)
print(LOFscore)
return LOFscore
#Data Generation
num_samples = 10
mu_x, sigma_x = 3, 2
data_x = np.random.normal(mu_x, sigma_x, num_samples)
mu_y, sigma_y = 1, 5
data_y = np.random.normal(mu_y, sigma_y, num_samples)
data = [[x, y] for (x, y) in zip(data_x, data_y)]
idx = range(num_samples)
# print(len(data))
df = pd.DataFrame(data, columns=['X', 'Y'], index=idx)
lof=LOF(data=data, nkp=3)
lof.k_dist()
lof.reachability_dist()
lof.lrd()
lofscore = lof.LOF_score()